
![[ Nobel Vật lý 2024 ] Cho những khám phá và phát minh nền tảng giúp thúc đẩy việc học máy với mạng nơ-ron nhân tạo [ Nobel Vật lý 2024 ] Cho những khám phá và phát minh nền tảng giúp thúc đẩy việc học máy với mạng nơ-ron nhân tạo](https://iirr.vn/wp-content/uploads/2024/10/rsz_670f301fb2635.png)
[ Nobel Vật lý 2024 ] Cho những khám phá và phát minh nền tảng giúp thúc đẩy việc học máy với mạng nơ-ron nhân tạo
For foundational discoveries and inventions that enable machine learning with artificial neural networks
![[ Nobel Vật lý 2024 ] Cho những khám phá và phát minh nền tảng giúp thúc đẩy việc học máy với mạng nơ-ron nhân tạo [ Nobel Vật lý 2024 ] Cho những khám phá và phát minh nền tảng giúp thúc đẩy việc học máy với mạng nơ-ron nhân tạo](https://iirr.vn/wp-content/uploads/2024/10/Hinh2_NobelVatLy2024.png)
[ Nobel Vật lý 2024 ] Cho những khám phá và phát minh nền tảng giúp thúc đẩy việc học máy với mạng nơ-ron nhân tạo
For foundational discoveries and inventions that enable machine learning with artificial neural networks
![[ Nobel Vật lý 2024 ] Cho những khám phá và phát minh nền tảng giúp thúc đẩy việc học máy với mạng nơ-ron nhân tạo [ Nobel Vật lý 2024 ] Cho những khám phá và phát minh nền tảng giúp thúc đẩy việc học máy với mạng nơ-ron nhân tạo](https://iirr.vn/wp-content/uploads/2024/10/Hinh1_NobelVatLy2024.png)
[ Nobel Vật lý 2024 ] Cho những khám phá và phát minh nền tảng giúp thúc đẩy việc học máy với mạng nơ-ron nhân tạo
For foundational discoveries and inventions that enable machine learning with artificial neural networks

![[ Nobel Vật lý 2024 ] Cho những khám phá và phát minh nền tảng giúp thúc đẩy việc học máy với mạng nơ-ron nhân tạo [ Nobel Vật lý 2024 ] Cho những khám phá và phát minh nền tảng giúp thúc đẩy việc học máy với mạng nơ-ron nhân tạo](https://iirr.vn/wp-content/uploads/2024/10/nobelvatly.png)
[ Nobel Vật lý 2024 ] Cho những khám phá và phát minh nền tảng giúp thúc đẩy việc học máy với mạng nơ-ron nhân tạo
For foundational discoveries and inventions that enable machine learning with artificial neural networks
Theo The Nobel Prize in Physics 2024: “For foundational discoveries and inventions that enable machine learning with artificial neural networks”
* * *
Viện Hàn lâm Khoa học Hoàng gia Thụy Điển đã quyết định trao Giải Nobel Vật lý năm 2024 chung cho
John J. Hopfield và Geoffrey E. Hinton
“Vì những khám phá và phát minh nền tảng giúp thúc đẩy việc học máy với mạng nơ-ron nhân tạo”
Giới thiệu
Với nguồn gốc từ những năm 1940, học máy dựa trên mạng nơ-ron nhân tạo (ANNs) đã phát triển trong ba thập kỷ qua thành một công cụ mạnh mẽ và linh hoạt, có ứng dụng trong cả đời sống hàng ngày và các ứng dụng khoa học tiên tiến. Với ANNs, biên giới của vật lý được mở rộng để bao trùm các hiện tượng của sự sống cũng như tính toán.
Được truyền cảm hứng từ các nơ-ron sinh học trong não, ANNs là tập hợp lớn các “nơ-ron” hoặc nút, được kết nối bởi các “khớp thần kinh” hoặc các kết nối có trọng số, được huấn luyện để thực hiện các nhiệm vụ nhất định thay vì làm theo một tập hợp các chỉ dẫn đã được xác định trước. Cấu trúc cơ bản của chúng có nhiều điểm tương đồng với các mô hình spin trong vật lý thống kê được áp dụng vào lý thuyết từ tính hoặc lý thuyết hợp kim. Giải Nobel Vật lý năm nay vinh danh những nghiên cứu khai thác mối liên hệ này để đạt được những đột phá phương pháp trong lĩnh vực ANN.
Bối cảnh lịch sử
Những máy tính điện tử đầu tiên xuất hiện vào những năm 1940 và được phát minh cho các mục đích quân sự và khoa học. Chúng được thiết kế để thực hiện các phép tính phức tạp và tốn thời gian mà con người khó có thể làm. Đến những năm 1950, một nhu cầu ngược lại xuất hiện: khiến máy tính thực hiện những gì mà con người và các loài động vật có vú khác giỏi – nhận diện mẫu (pattern recognition).
Mục tiêu hướng tới trí tuệ nhân tạo này ban đầu được tiếp cận bởi các nhà toán học và các nhà khoa học máy tính, những người phát triển các chương trình dựa trên các quy tắc logic. Cách tiếp cận này được tiếp tục cho đến những năm 1980, nhưng các nguồn tài nguyên tính toán cần thiết cho việc phân loại chính xác, chẳng hạn như hình ảnh, trở nên quá đắt đỏ.
Song song đó, những nỗ lực đã được bắt đầu nhằm tìm hiểu cách các hệ thống sinh học giải quyết vấn đề nhận diện mẫu. Ngay từ năm 1943, Warren McCulloch và Walter Pitts [1], một nhà thần kinh học và một nhà logic học, đã đề xuất một mô hình về cách các nơ-ron trong não hợp tác với nhau. Trong mô hình của họ, một nơ-ron hình thành tổng trọng số của các tín hiệu nhị phân đến từ các nơ-ron khác, từ đó xác định tín hiệu nhị phân ra đi. Công trình của họ trở thành nền tảng cho nghiên cứu sau này về cả mạng nơ-ron sinh học và nhân tạo.
Một đóng góp quan trọng khác đến từ nhà tâm lý học Donald Hebb [2]. Vào năm 1949, Hebb đề xuất một cơ chế học tập và ghi nhớ, trong đó sự kích hoạt đồng thời và lặp lại của hai nơ-ron dẫn đến sự tăng cường mạnh mẽ của khớp thần kinh giữa chúng.
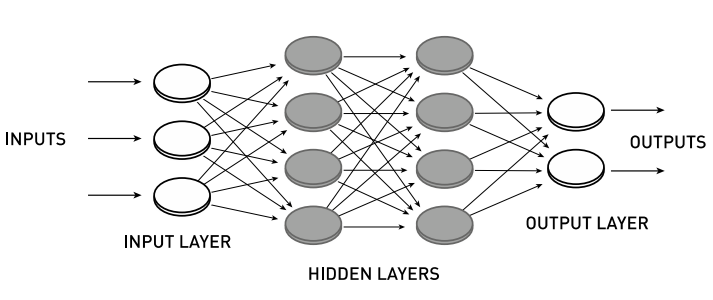
Trong lĩnh vực mạng nơ-ron nhân tạo (ANN), hai kiến trúc cho các hệ thống nút kết nối đã được khám phá: mạng hồi tiếp (recurrent) và mạng tiến tới (feedforward), trong đó mạng hồi tiếp cho phép sự tương tác phản hồi (Hình 1 và 2). Mạng tiến tới có lớp đầu vào và đầu ra, và có thể chứa thêm các lớp ẩn xen giữa.
Năm 1957, Frank Rosenblatt đã đề xuất một mạng tiến tới cho việc diễn giải hình ảnh, cũng được thực hiện bằng phần cứng máy tính [3]. Hệ thống này có ba lớp nút, với trọng số có thể điều chỉnh chỉ giữa các lớp giữa và lớp đầu ra. Những trọng số này được xác định một cách hệ thống.
Hệ thống của Rosenblatt thu hút nhiều sự chú ý nhưng có giới hạn khi giải quyết các bài toán phi tuyến tính. Một ví dụ đơn giản là bài toán “một hoặc cái này nhưng không phải cả hai” (bài toán XOR). Những giới hạn này đã được chỉ ra trong một cuốn sách có ảnh hưởng của Marvin Minsky và Seymour Papert vào năm 1969 [4], dẫn đến việc nghiên cứu ANN bị gián đoạn do thiếu kinh phí.
Một sự phát triển song song lấy cảm hứng từ các hệ thống từ tính, nhằm tạo ra các mô hình mạng nơ-ron hồi tiếp và nghiên cứu các tính chất tập thể của chúng [5-10].
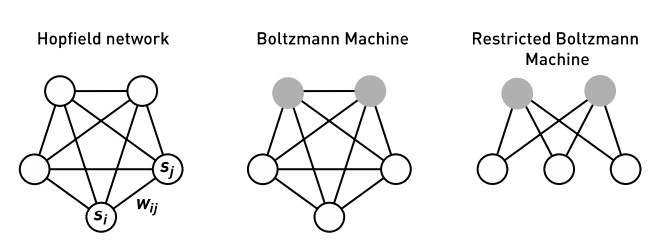
Hình 1. Các mạng hồi tiếp với N nút nhị phân Si (0 hoặc 1), với các trọng số kết nối Wij. (Trái) Mô hình Hopfield. (Giữa) Máy Boltzmann. Các nút được chia thành hai nhóm, nút nhìn thấy (hình tròn rỗng) và nút ẩn (hình tròn màu xám). Mạng lưới này được huấn luyện để xấp xỉ phân bố xác suất của một tập hợp các mẫu nhìn thấy. Sau khi huấn luyện, mạng có thể được sử dụng để tạo ra các mẫu mới từ phân bố đã học. (Phải) Máy Boltzmann Hạn chế (RBM). Giống như máy Boltzmann, nhưng không có sự kết nối bên trong lớp nhìn thấy hoặc giữa các nút ẩn. Phiên bản này có thể được sử dụng để huấn luyện trước từng lớp cho các mạng sâu.
Những năm 1980
Thập niên 1980 chứng kiến những đột phá lớn trong cả hai lĩnh vực mạng nơ-ron hồi tiếp và tiến tới, dẫn đến sự mở rộng nhanh chóng của lĩnh vực ANN.
John Hopfield, một nhà vật lý lý thuyết, là một nhân vật nổi bật trong vật lý sinh học. Công trình quan trọng của ông vào thập niên 1970 đã kiểm tra sự truyền electron giữa các phân tử sinh học [11] và sự sửa lỗi trong các phản ứng sinh hóa (quá trình kiểm chứng động học) [12].
Vào năm 1982, Hopfield đã công bố một mô hình động lực học về bộ nhớ liên kết dựa trên một mạng nơ-ron hồi tiếp đơn giản [13]. Các hiện tượng tập thể thường xuất hiện trong các hệ thống vật lý, chẳng hạn như các miền từ trong hệ thống từ tính và các xoáy trong dòng chảy chất lỏng. Hopfield đặt câu hỏi liệu các hiện tượng tập thể này trong các tập hợp lớn các nơ-ron có thể mang lại khả năng “tính toán” hay không.
Lưu ý rằng các tính chất tập thể trong nhiều hệ thống vật lý ổn định đối với những thay đổi trong các chi tiết của mô hình, ông đã giải quyết câu hỏi này bằng cách sử dụng một mạng nơ-ron với N nút nhị phân Si (0 hoặc 1). Động lực học là bất đối xứng với các cập nhật ngưỡng của từng nút riêng lẻ theo các thời điểm ngẫu nhiên. Giá trị mới của một nút Si được xác định bởi tổng trọng số của tất cả các nút khác:
hi = ∑(j ≠ i) Wij Sj
và được đặt thành Si = 1 nếu hi > 0, và Si = 0 nếu ngược lại (ngưỡng được đặt bằng 0). Các trọng số Wij được giả định là đối xứng và phản ánh mối tương quan cặp giữa các nút trong các bộ nhớ đã được lưu trữ, được gọi là quy tắc Hebb. Sự đối xứng của các trọng số đảm bảo động lực học ổn định. Các trạng thái dừng được xác định là các ký ức, phân bố trên N nút trong một dạng lưu trữ phi cục bộ. Hơn nữa, mạng lưới được gán một năng lượng E, được cho bởi:
E = – ∑(i < j) Wij Si Sj
đây là một hàm giảm đơn điệu dưới động lực học của mạng lưới. Điều đáng chú ý là mối liên hệ giữa thế giới vật lý, như đã được định nghĩa vào thập niên 1980, và mạng nơ-ron nhân tạo (ANNs) đã trở nên rõ ràng ngay từ hai phương trình này. Phương trình đầu tiên có thể được sử dụng để biểu diễn trường phân tử của Weiss (được đặt theo tên của nhà vật lý người Pháp Pierre Weiss), mô tả cách các mômen từ nguyên tử liên kết trong một chất rắn, và phương trình sau được sử dụng để đánh giá năng lượng của một cấu hình từ, ví dụ như trong chất sắt từ. Hopfield đã hiểu rõ cách các phương trình này có thể được sử dụng để mô tả các vật liệu từ tính.
Về mặt ẩn dụ, động lực học dẫn hệ thống với N nút đến các thung lũng trong không gian năng lượng N chiều, nơi các trạng thái dừng được xác định. Các trạng thái dừng này đại diện cho các ký ức đã học theo quy tắc Hebb. Ban đầu, số lượng ký ức có thể được lưu trữ trong mô hình động lực học của Hopfield là có giới hạn. Các phương pháp để giải quyết vấn đề này đã được phát triển trong các nghiên cứu sau [14].
Hopfield đã sử dụng mô hình của mình như một bộ nhớ liên kết hoặc một phương pháp sửa lỗi hoặc hoàn thiện mẫu. Một hệ thống khởi tạo với một mẫu không chính xác, chẳng hạn như một từ bị viết sai chính tả, sẽ bị thu hút về điểm cực tiểu năng lượng cục bộ gần nhất trong mô hình của ông, qua đó xảy ra sự sửa chữa. Mô hình này đã thu hút sự chú ý khi người ta nhận ra rằng các tính chất cơ bản, chẳng hạn như khả năng lưu trữ, có thể được hiểu phân tích bằng các phương pháp từ lý thuyết spin thủy tinh [15, 16].
Một câu hỏi hợp lý vào thời điểm đó là liệu các tính chất của mô hình này có phải là hiện tượng đặc biệt của cấu trúc nhị phân thô sơ hay không. Hopfield đã trả lời câu hỏi này bằng cách tạo ra một phiên bản tương tự của mô hình [17], với động lực học thời gian liên tục. Phân tích của ông chỉ ra rằng các nút nhị phân có thể được thay thế bằng các nút tương tự mà không làm mất đi các tính chất tập thể của mô hình gốc.
Các trạng thái dừng của mô hình tương tự tương ứng với các nghiệm trường trung bình của hệ nhị phân ở nhiệt độ hiệu dụng có thể điều chỉnh, và tiến gần đến các trạng thái dừng của mô hình nhị phân ở nhiệt độ thấp.
Sự tương đồng chặt chẽ giữa các mô hình tương tự và nhị phân sau đó đã được Hopfield và David Tank [18, 19] sử dụng để phát triển một phương pháp giải quyết các bài toán tối ưu hóa rời rạc khó dựa trên động lực học thời gian liên tục của mô hình tương tự. Ở đây, bài toán tối ưu hóa cần giải quyết, bao gồm các ràng buộc, được mã hóa trong các tham số tương tác (các trọng số) của mạng lưới. Họ chọn sử dụng động lực học của mô hình tương tự để có một “bề mặt năng lượng mềm” hơn, qua đó tạo điều kiện thuận lợi cho việc tìm kiếm. Nhiệt độ hiệu dụng của hệ tương tự được giảm dần, giống như trong tối ưu hóa toàn cầu với phương pháp ủ mô phỏng (simulated annealing) [20]. Tối ưu hóa xảy ra thông qua việc tích hợp các phương trình chuyển động của một mạch điện tử, trong đó các nút tiến hóa mà không cần hướng dẫn từ một đơn vị trung tâm. Phương pháp này là một ví dụ tiên phong về việc sử dụng hệ thống động lực học để tìm kiếm lời giải cho các bài toán tối ưu hóa rời rạc khó [21]. Một ví dụ gần đây hơn là ủ lượng tử (quantum annealing) [22].
Bằng cách tạo ra và khám phá các mô hình động lực học dựa trên vật lý này – không chỉ mô hình bộ nhớ liên kết cột mốc mà cả những mô hình tiếp theo – Hopfield đã đóng góp nền tảng quan trọng cho sự hiểu biết của chúng ta về khả năng tính toán của mạng nơ-ron.
Từ năm 1983 đến năm 1985, Geoffrey Hinton, cùng với Terrence Sejnowski và các đồng nghiệp khác, đã phát triển một phần mở rộng ngẫu nhiên của mô hình Hopfield từ năm 1982, gọi là máy Boltzmann [23, 24]. Ở đây, mỗi trạng thái s=(s1, s2, …, sN) của mạng được gán một xác suất theo phân bố Boltzmann:
P(s) ∝ e^(-E/T)
E = – ∑(i < j) Wij Si Sj – ∑i θi Si
trong đó T là nhiệt độ giả định và θi là trường cục bộ, hoặc độ lệch.
Máy Boltzmann là một mô hình sinh (generative model). Không giống như mô hình Hopfield, nó tập trung vào phân bố xác suất của các mẫu thay vì các mẫu riêng lẻ. Nó chứa các nút nhìn thấy tương ứng với các mẫu cần học cũng như các nút ẩn, giúp mở rộng khả năng mô hình hóa các phân bố xác suất tổng quát hơn.
Hình 2. Mạng tiến tới với hai lớp nút ẩn giữa các lớp đầu vào và đầu ra.
Các tham số trọng số và độ lệch của mạng, xác định năng lượng E, được điều chỉnh sao cho phân bố xác suất của các mẫu nhìn thấy được tạo ra bởi mô hình chỉ lệch rất ít so với phân bố xác suất thống kê của một tập hợp các mẫu huấn luyện nhất định. Hinton và các đồng nghiệp đã phát triển một thuật toán học tinh tế, dựa trên độ dốc, để xác định các tham số này [24]; tuy nhiên, mỗi bước của thuật toán này bao gồm các mô phỏng trạng thái cân bằng tốn thời gian cho hai tập hợp khác nhau.
Mặc dù có sự quan tâm về mặt lý thuyết, trên thực tế, máy Boltzmann ban đầu chỉ được sử dụng hạn chế. Tuy nhiên, một phiên bản đơn giản hóa với ít trọng số hơn, gọi là máy Boltzmann hạn chế (restricted Boltzmann machine), đã được phát triển thành một công cụ linh hoạt (xem phần tiếp theo).
Cả mô hình Hopfield và máy Boltzmann đều là các mạng nơ-ron hồi tiếp. Những năm 1980 cũng chứng kiến những tiến bộ quan trọng về mạng tiến tới. Một bước tiến quan trọng là minh chứng của David Rumelhart, Hinton và Ronald Williams vào năm 1986 về cách các kiến trúc có một hoặc nhiều lớp nút ẩn có thể được huấn luyện để phân loại bằng cách sử dụng một thuật toán được biết đến như là lan truyền ngược (backpropagation) [25]. Ở đây, mục tiêu là giảm thiểu độ lệch trung bình bình phương D giữa đầu ra từ mạng và dữ liệu huấn luyện, bằng cách tối ưu hóa độ dốc. Điều này đòi hỏi tính đạo hàm riêng của D đối với tất cả các trọng số trong mạng. Rumelhart, Hinton và Williams đã sáng tạo lại cách tiếp cận này, vốn trước đây được áp dụng cho các vấn đề liên quan bởi những người khác [26, 27]. Quan trọng hơn nữa, họ đã chứng minh rằng các mạng với một lớp nút ẩn có thể được huấn luyện bằng phương pháp này để thực hiện các nhiệm vụ mà không thể giải quyết được nếu thiếu lớp đó. Ngoài ra, họ đã làm sáng tỏ chức năng của các nút ẩn.
Hướng tới học sâu
Những đột phá phương pháp luận vào thập niên 1980 đã nhanh chóng được tiếp nối bởi các ứng dụng thành công, bao gồm nhận diện mẫu trong hình ảnh, ngôn ngữ và dữ liệu lâm sàng. Một phương pháp quan trọng là mạng nơ-ron tích chập nhiều lớp (CNN) được huấn luyện bằng thuật toán lan truyền ngược, do Yann LeCun và Yoshua Bengio thúc đẩy [28, 29]. Kiến trúc CNN có nguồn gốc từ neocognitron do Kunihiko Fukushima phát minh [30], người lấy cảm hứng từ công trình của David Hubel và Torsten Wiesel, những người đoạt giải Nobel Y học vào năm 1981. Phương pháp CNN được phát triển bởi LeCun và các đồng nghiệp đã được nhiều ngân hàng Mỹ sử dụng từ giữa thập niên 1990 để phân loại các chữ số viết tay trên séc. Một ví dụ thành công khác từ thời kỳ này là phương pháp bộ nhớ dài-ngắn hạn (long short-term memory – LSTM), được tạo ra bởi Sepp Hochreiter và Jürgen Schmidhuber [31]. Đây là một mạng hồi tiếp để xử lý dữ liệu tuần tự, chẳng hạn như ngôn ngữ và lời nói, và có thể được ánh xạ thành một mạng nhiều lớp thông qua việc “mở rộng thời gian”.
Mặc dù một số kiến trúc nhiều lớp đã dẫn đến các ứng dụng thành công trong thập niên 1990, việc huấn luyện các mạng sâu với nhiều lớp kết nối vẫn là một thách thức. Đối với nhiều nhà nghiên cứu trong lĩnh vực này, việc huấn luyện các mạng nhiều lớp dày đặc dường như là điều bất khả thi. Tuy nhiên, tình hình đã thay đổi vào những năm 2000. Một trong những người dẫn đầu trong đột phá này là Hinton, và một công cụ quan trọng là máy Boltzmann hạn chế (RBM).
Mạng RBM chỉ có trọng số giữa các nút nhìn thấy và các nút ẩn, và không có trọng số kết nối giữa hai nút cùng loại. Đối với RBMs, Hinton đã tạo ra một thuật toán học gần đúng hiệu quả gọi là phân kỳ đối lập (contrastive divergence) [32], nhanh hơn nhiều so với thuật toán của máy Boltzmann đầy đủ [24]. Cùng với Simon Osindero và Yee-Whye Teh, Hinton sau đó đã phát triển một quy trình huấn luyện cho các mạng nhiều lớp, trong đó các lớp được huấn luyện từng lớp một bằng cách sử dụng RBM [33]. Một ứng dụng ban đầu của phương pháp này là mạng autoencoder để giảm chiều [34, 35]. Sau khi huấn luyện trước, có thể thực hiện tinh chỉnh tham số toàn cầu bằng cách sử dụng thuật toán lan truyền ngược. Việc huấn luyện trước với RBMs nắm bắt các cấu trúc trong dữ liệu, chẳng hạn như các góc trong hình ảnh, mà không sử dụng dữ liệu huấn luyện có nhãn. Sau khi tìm thấy các cấu trúc này, việc gán nhãn bằng thuật toán lan truyền ngược trở nên tương đối đơn giản.
Bằng cách liên kết các lớp đã được huấn luyện trước theo cách này, Hinton đã có thể triển khai thành công các ví dụ về mạng sâu và dày đặc, đánh dấu một cột mốc hướng tới cái mà ngày nay được biết đến là học sâu. Sau này, đã có thể thay thế việc huấn luyện trước bằng RBM bằng các phương pháp khác để đạt được hiệu suất tương tự trên các mạng ANN dày đặc và sâu.
ANNs như những công cụ mạnh mẽ trong vật lý và các ngành khoa học khác
Phần lớn các thảo luận trên tập trung vào cách vật lý là động lực thúc đẩy những phát minh và sự phát triển của ANNs. Ngược lại, ANNs hiện đang đóng một vai trò quan trọng như một công cụ mạnh mẽ cho việc mô hình hóa và phân tích trong hầu hết các lĩnh vực vật lý.
Trong một số ứng dụng, ANNs được sử dụng như một công cụ xấp xỉ hàm [36]; nghĩa là, ANNs được dùng để tạo ra một “bản sao” cho mô hình vật lý đang được nghiên cứu. Điều này có thể giảm đáng kể các tài nguyên tính toán cần thiết, cho phép các hệ thống lớn hơn được kiểm tra ở độ phân giải cao hơn. Những tiến bộ đáng kể đã đạt được trong lĩnh vực này, ví dụ như cho các bài toán lượng tử nhiều thân [37-39]. Tại đây, các kiến trúc học sâu được huấn luyện để tái tạo các năng lượng của các pha vật chất, cũng như hình dạng và độ mạnh của các lực tương tác, với độ chính xác tương đương với các mô hình lượng tử học ab initio. Với các mô hình ANNs đã được huấn luyện này, việc xác định sự ổn định pha và động lực học của các vật liệu mới trở nên nhanh hơn đáng kể. Các ví dụ minh họa thành công của những phương pháp này bao gồm dự đoán các vật liệu quang điện mới.
Với các mô hình này, cũng có thể nghiên cứu các chuyển pha [40] cũng như các tính chất nhiệt động lực học của nước [41]. Tương tự, sự phát triển của các biểu diễn ANN đã giúp đạt được độ phân giải cao hơn trong các mô hình khí hậu dựa trên vật lý [42, 43] mà không cần sử dụng thêm tài nguyên tính toán.
Trong những năm 1990, ANNs đã trở thành một công cụ phân tích dữ liệu tiêu chuẩn trong các thí nghiệm vật lý hạt với độ phức tạp ngày càng cao. Các hạt cơ bản được săn tìm, chẳng hạn như boson Higgs, chỉ tồn tại trong một phần nhỏ của giây sau khi được tạo ra trong các vụ va chạm năng lượng cao (ví dụ, ~10^-22 s đối với boson Higgs). Sự hiện diện của chúng cần phải được suy luận từ các dấu vết ion hóa và năng lượng lắng đọng trong các máy dò điện tử lớn. Thường thì chữ ký của máy dò dự đoán là rất hiếm và có thể bị bắt chước bởi các quá trình nền phổ biến hơn. Để nhận diện các quá trình phân rã hạt và tăng hiệu suất phân tích, ANNs đã được huấn luyện để chọn ra các mẫu cụ thể trong lượng dữ liệu lớn được tạo ra từ các máy dò với tốc độ cao.
ANNs đã cải thiện độ nhạy trong việc tìm kiếm boson Higgs tại Máy Gia tốc Điện tử-Vị trí Lớn (LEP) của CERN trong những năm 1990 [44], và đã được sử dụng trong phân tích dữ liệu dẫn đến việc phát hiện boson Higgs tại Máy Gia tốc Hạt Lớn của CERN vào năm 2012 [45]. ANNs cũng được sử dụng trong các nghiên cứu về hạt quark top tại Fermilab [46].
Trong vật lý thiên văn và thiên văn học
Trong vật lý thiên văn và thiên văn học, ANNs cũng đã trở thành một công cụ phân tích dữ liệu tiêu chuẩn. Một ví dụ gần đây là việc phân tích dữ liệu bằng ANN từ máy dò neutrino IceCube tại Nam Cực, kết quả là tạo ra một hình ảnh neutrino của Dải Ngân hà [47]. Các hành tinh ngoài hệ Mặt trời đã được xác định bởi Sứ mệnh Kepler bằng cách sử dụng ANNs [48]. Hình ảnh từ Kính viễn vọng Chân trời Sự kiện về hố đen tại trung tâm Dải Ngân hà cũng đã sử dụng ANNs để xử lý dữ liệu [49].
Cho đến nay, bước đột phá khoa học nổi bật nhất sử dụng các phương pháp học sâu dựa trên ANNs là công cụ AlphaFold để dự đoán cấu trúc ba chiều của protein từ chuỗi axit amin của chúng [50]. Trong lĩnh vực vật lý công nghiệp và hóa học, ANNs cũng đóng vai trò ngày càng quan trọng.
ANNs trong cuộc sống hàng ngày
Danh sách các ứng dụng được sử dụng trong cuộc sống hàng ngày dựa trên ANNs rất dài. Các mạng này đứng đằng sau hầu hết mọi thứ mà chúng ta làm với máy tính, chẳng hạn như nhận diện hình ảnh, tạo ngôn ngữ, và nhiều hơn nữa.
Hỗ trợ ra quyết định trong lĩnh vực y tế cũng là một ứng dụng đã được thiết lập tốt của ANNs. Ví dụ, một nghiên cứu ngẫu nhiên có triển vọng gần đây về sàng lọc hình ảnh chụp quang tuyến vú đã chỉ ra lợi ích rõ ràng của việc sử dụng học máy trong việc cải thiện phát hiện ung thư vú [51]. Một ví dụ khác gần đây là việc điều chỉnh chuyển động cho chụp cộng hưởng từ (MRI) [52].
Nhận xét và kết luận
Các phương pháp và ý tưởng tiên phong được phát triển bởi Hopfield và Hinton đã đóng vai trò quan trọng trong việc định hình lĩnh vực ANNs. Ngoài ra, Hinton đã đóng một vai trò lãnh đạo trong các nỗ lực mở rộng các phương pháp này cho các ANNs dày đặc và sâu.
Với những đột phá này, dựa trên nền tảng của khoa học vật lý, họ đã chỉ ra một cách hoàn toàn mới để chúng ta sử dụng máy tính để hỗ trợ và hướng dẫn chúng ta đối mặt với nhiều thách thức mà xã hội đang đối mặt. Nói một cách đơn giản, nhờ có công trình của họ, nhân loại hiện có một công cụ mới trong hộp công cụ của mình, mà chúng ta có thể sử dụng cho những mục đích tốt. Học máy dựa trên ANNs hiện đang cách mạng hóa khoa học, kỹ thuật, và đời sống hàng ngày. Lĩnh vực này đã sẵn sàng để tạo ra những đột phá mới hướng tới việc xây dựng một xã hội bền vững, ví dụ như giúp xác định các vật liệu mới có chức năng. Học sâu bằng ANNs sẽ được sử dụng trong tương lai để quyết định cách con người chọn sử dụng những công cụ mạnh mẽ đáng kinh ngạc này, vốn đã hiện diện trong nhiều khía cạnh của cuộc sống chúng ta.
Tài liệu tham khảo
1. W.S. McCulloch and W. Pitts, Bull. Math. Biophys. 5, 115 (1943).
2. D.O. Hebb, The organization of behavior (Wiley & Sons, New York, 1949).
3. F. Rosenblatt, Principles of neurodynamics: Perceptrons and theory of brain mechanisms (Spartan Book, Washington D.C., 1962).
4. M.L. Minsky and S.A. Papert, Perceptrons: An introduction to computational geometry (MIT Press, Cambridge, 1969).
5. B.G. Cragg and H.N.V. Temepley, Brain 78, 304 (1955).
6. E.R. Caianiello, J. Theor. Biol. 2, 204 (1961).
7. K. Nakano, IEEE Trans., Syst., Man, Cybern. SMC-2, 380 (1972).
8. S.-I. Amari, IEEE Trans. Comput. C-21, 1197 (1972).
9. W.A. Little, Math. Biosci. 19, 101 (1974).
10. W.A. Little and G.L. Shaw, Math. Biosci. 39, 281 (1978).
11. J.J. Hopfield, Proc. Natl. Acad. Sci USA 71, 3640 (1974).
12. J.J. Hopfield, Proc. Natl. Acad. Sci USA 71, 4135 (1974).
13. J.J. Hopfield, Proc. Natl. Acad. Sci USA 79, 2554 (1982).
14. D.D. Krotov and J.J. Hopfield. In Advances in Neural Information Processing Systems 29, 1172 (2016).
15. D. J. Amit, H. Gutfreund and H. Sompolinsky, Phys. Rev. A 32, 1007 (1985).
16. M. Mézard, G. Parisi and M. Virasoro, Spin glass theory and beyond: An introduction to the replica method and its applications (World Scientific, Singapore, 1987).
17. J.J. Hopfield, Proc. Natl. Acad. Sci USA 81, 3088 (1984).
18. J.J. Hopfield and D.W. Tank, Biol. Cybern. 52, 141 (1985).
19. J.J. Hopfield and D.W. Tank, Science 233, 625 (1986).
20. S. Kirkpatrick, C.D. Gelatt and M.P. Vecchi, Science 220, 671 (1983).
21. N. Mohseni, P. McMahon and T. Byrnes, Nat. Rev. Phys. 4, 363 (2022).
22. T. Kadokawi and H. Nishimori, Phys. Rev. E 58, 5355 (1998).
23. S.E. Fahlman, G.E. Hinton and T.J. Sejnowski. In Proceedings of the AAAI-83 conference, pp. 109-113 (1983).
24. D.H. Ackley, G.E. Hinton and T.J. Sejnowski, Cogn Sci. 9, 147 (1985).
25. D.E. Rumelhart, G.E. Hinton and R.J. Williams, Nature 323, 533 (1986).
26. P.J. Werbos. In System Modeling and Optimization, pp. 762-770 (1982).
27. S. Linnainmaa, Master’s thesis (in Finnish), Univ. Helsinki (1970); published in BIT 16, 146 (1976).
28. Y. LeCun, B.Boser, J.S. Denker, D. Henderson, R.E. Howard, W. Hubbard and L.D. Jackel, Neural Comput. 1, 541 (1989).
29. Y. LeCun, L. Bottou, Y. Bengio and P. Haffner, Proc. IEEE 86, 2278 (1998).
30. K. Fukushima, Biol. Cybern. 36, 193 (1980).
31. S. Hochreiter and J. Schmidhuber, Neural Comput. 9, 1735 (1997).
32. G.E. Hinton, Neural Comput. 14, 1771 (2002).
33. G.E. Hinton, S. Osindero and Y.-W. The, Neural Comput. 18, 1527 (2006).
34. Y. Bengio, P. Lamblin, D. Popovici and H. Larochelle. In Advances in Neural Information Processing Systems 19, 153 (2006).
35. G.E. Hinton and R. Salakhutdinov, Science 313, 504 (2006).
36. K. Hornik, Neural Net. 4, 251 (1991).
37. J. Behler and M. Parrinello, Phys. Rev. Lett. 98, 146401 (2007).
38. G. Carleo and M. Troyer, Science 355, 602 (2017).
39. P.M. Piaggi, J. Wes, A.Z. Panagiotopoulos, P.G. Debenedetti and R. Car, Proc. Natl. Acad. Sci. USA 119, e2207294119 (2022).
40. R. Jinnouchi, J. Lahnstener, F. Karsai, G. Kresse and M. Bokdam, Phys. Rev. Lett. 122, 225701 (2019).
41. P.M. de Hijes, C. Dellago, R. Jinnouchi, B. Schmidayer and G. Kresse, J. Chem. Phys. 160, 114107 (2024).
42. S. Rasp, M.S. Pritchard and P. Gentine, Proc. Natl. Acad. Sci USA 115, 9684 (2018).
43. C. Wong, Nature 628, 710 (2024).
44. ALEPH Collaborations, Phys. Lett B 447, 336 (1999).
45. ATLAS Collaboration, Phys. Lett. B 716, 1 (2012).
46. D0 Collaboration, Phys. Rev. Lett. 103, 092001 (2009).
47. IceCube Collaboration, Science 380, 1338 (2023).
48. K.A. Pearson, L. Palafox and C.A. Griffith, Mon. Not. R. Astron. Soc. 474, 478 (2017).
49. EHT Collaboration, ApJL 930, L15 (2022).
50. J. Jumper et al., Nature 596, 583 (2021).
51. K. Láng et al., Lancet Oncol. 24, 936 (2023).
52. V. Spieker et al., IEEE Trans. Med. Imaging 43, 846 (2024).
Thuật ngữ chuyên ngành và định nghĩa cơ bản
1. Mạng nơ-ron nhân tạo (ANN – Artificial Neural Network):
Mô hình tính toán lấy cảm hứng từ hoạt động của nơ-ron sinh học trong não người, bao gồm các nút (nơ-ron) được kết nối với nhau bằng các khớp thần kinh (các trọng số). Các mạng nơ-ron này có thể được huấn luyện để thực hiện các nhiệm vụ như nhận dạng mẫu, phân loại dữ liệu, hoặc dự đoán.2. Lan truyền ngược (Backpropagation):
Định nghĩa: Một thuật toán huấn luyện mạng nơ-ron nhân tạo thông qua việc tính toán đạo hàm và điều chỉnh trọng số dựa trên lỗi giữa đầu ra dự đoán và đầu ra thực tế.3. Máy Boltzmann (Boltzmann Machine):
Định nghĩa: Một loại mạng nơ-ron hồi tiếp trong đó mỗi trạng thái của mạng được gán một xác suất theo phân bố Boltzmann. Mô hình này tập trung vào phân bố xác suất của các mẫu dữ liệu thay vì xử lý từng mẫu riêng lẻ.4. Máy Boltzmann hạn chế (RBM – Restricted Boltzmann Machine):
Định nghĩa: Phiên bản đơn giản hóa của máy Boltzmann, trong đó các nút cùng loại (nhìn thấy hoặc ẩn) không có kết nối với nhau, giúp giảm bớt độ phức tạp của bài toán huấn luyện.5. Học sâu (Deep Learning):
Định nghĩa: Một nhánh của học máy, trong đó các mạng nơ-ron với nhiều lớp ẩn (deep neural networks) được huấn luyện để thực hiện các nhiệm vụ phức tạp hơn, chẳng hạn như nhận diện hình ảnh hoặc dịch ngôn ngữ.6. Neutrino:
Định nghĩa: Một hạt hạ nguyên tử không mang điện tích và rất nhẹ, được tạo ra trong quá trình phân rã phóng xạ và các phản ứng hạt nhân.7. Xấp xỉ hàm (Function Approximation):
Định nghĩa: Một quá trình trong đó các mô hình (như ANN) được sử dụng để dự đoán hoặc tái tạo các giá trị hàm phức tạp bằng cách xấp xỉ giá trị dựa trên dữ liệu huấn luyện.8. AlphaFold:
Định nghĩa: Một hệ thống học sâu được phát triển bởi DeepMind, sử dụng mạng nơ-ron để dự đoán cấu trúc ba chiều của protein từ chuỗi axit amin của chúng.9. Lan truyền tiến (Feedforward):
Định nghĩa: Mô hình mạng nơ-ron trong đó tín hiệu di chuyển theo một hướng duy nhất từ lớp đầu vào qua các lớp ẩn đến lớp đầu ra, không có phản hồi ngược.10. Suy luận Bayes (Bayesian Inference):
Định nghĩa: Một phương pháp suy luận thống kê, trong đó các xác suất được cập nhật khi có thêm dữ liệu mới. Đây là nền tảng cho các mô hình như máy Boltzmann.11. Quantum Annealing (Ủ lượng tử):
Định nghĩa: Một kỹ thuật tối ưu hóa toàn cục dựa trên các nguyên lý lượng tử, sử dụng để giải quyết các bài toán tối ưu hóa phức tạp.12. LSTM (Long Short-Term Memory):
Định nghĩa: Một loại mạng nơ-ron hồi tiếp được thiết kế để ghi nhớ thông tin trong thời gian dài, xử lý các dữ liệu tuần tự như chuỗi văn bản hoặc âm thanh.13. Hạt quark top:
Định nghĩa: Một trong sáu hạt quark cơ bản trong mô hình chuẩn của vật lý hạt, có khối lượng lớn nhất trong các hạt quark.14. Boson Higgs:
Định nghĩa: Một hạt hạ nguyên tử được cho là có vai trò trong việc tạo ra khối lượng cho các hạt khác thông qua cơ chế Higgs.









