

Các phương pháp thực nghiệm tạo ra xung ánh sáng attosecond để nghiên cứu động lực học điện tử trong vật chất
For experimental methods that generate attosecond pulses of light for the study of electron dynamics in matter
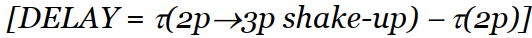
Các phương pháp thực nghiệm tạo ra xung ánh sáng attosecond để nghiên cứu động lực học điện tử trong vật chất
For experimental methods that generate attosecond pulses of light for the study of electron dynamics in matter

Các phương pháp thực nghiệm tạo ra xung ánh sáng attosecond để nghiên cứu động lực học điện tử trong vật chất
For experimental methods that generate attosecond pulses of light for the study of electron dynamics in matter

Các phương pháp thực nghiệm tạo ra xung ánh sáng attosecond để nghiên cứu động lực học điện tử trong vật chất
For experimental methods that generate attosecond pulses of light for the study of electron dynamics in matter

Các phương pháp thực nghiệm tạo ra xung ánh sáng attosecond để nghiên cứu động lực học điện tử trong vật chất
For experimental methods that generate attosecond pulses of light for the study of electron dynamics in matter


Các phương pháp thực nghiệm tạo ra xung ánh sáng attosecond để nghiên cứu động lực học điện tử trong vật chất
For experimental methods that generate attosecond pulses of light for the study of electron dynamics in matter


Các phương pháp thực nghiệm tạo ra xung ánh sáng attosecond để nghiên cứu động lực học điện tử trong vật chất
For experimental methods that generate attosecond pulses of light for the study of electron dynamics in matter

Các phương pháp thực nghiệm tạo ra xung ánh sáng attosecond để nghiên cứu động lực học điện tử trong vật chất
For experimental methods that generate attosecond pulses of light for the study of electron dynamics in matter
Bài viết gốc (ENG): The Nobel Prize in Physics 2023 – Advanced information
Thông cáo báo chí: The Nobel Prize in Physics 2023 – Experiments with light capture the shortest of moments
Học viện Khoa học Hoàng gia Thụy Điển đã quyết định trao Giải Nobel Vật lý năm 2023
đồng thời cho Pierre Agostini, Ferenc Krausz và Anne L’Huillier.
CÁC PHƯƠNG PHÁP THỰC NGHIỆM TẠO RA XUNG ÁNH SÁNG ATTOSECOND
ĐỂ NGHIÊN CỨU ĐỘNG LỰC HỌC ĐIỆN TỬ TRONG VẬT CHẤT
* * *
Bối cảnh
Giải thưởng Nobel Vật lý năm 2023 được trao cho nghiên cứu về chuyển động của electron trong nguyên tử, phân tử và vật chất ở pha ngưng tụ bằng phương pháp quang phổ attosecond (atto giây – một phần triệu tỷ tỷ, tương đương 10−18).
Khi Werner Heisenberg sáng tạo lý thuyết cơ học lượng tử mới vào năm 1925 [1], lập luận chính của ông là lý thuyết cơ học lượng tử cũ, buộc các nhà vật lý phải sử dụng các đại lượng mà về nguyên tắc không thể quan sát được, như vị trí và chu kỳ quay của electron trong nguyên tử hydro. Heisenberg lập luận rằng một lý thuyết mới nên dựa trên các “đại lượng quan sát được”, chẳng hạn như tần số của các quá trình chuyển đổi lượng tử.
Bài báo trực quan của Heisenberg năm 1925 là một trong những bài báo quan trọng nhất trong vật lý học thế kỷ 20, nhưng điều ông không thể lường trước được là những gì từng “về nguyên tắc” là không thể quan sát được giờ đây đang dần có thể tiếp cận trong các thí nghiệm tại phòng thí nghiệm. Mặc dù chúng ta có thể chưa thể quan sát, theo nghĩa chặt chẽ, vị trí và chuyển động quay của một electron xung quanh hạt nhân, nhưng ngày nay, chúng ta có thể “nhìn thấy” động lực học của electron trong nguyên tử, phân tử và vật chất ở pha ngưng tụ trong các thí nghiệm tại phòng thí nghiệm.
Điều này có thể thực hiện như thế nào? Các lập luận đơn giản dựa trên việc so sánh đơn vị thời gian nguyên tử nội tại, khoảng 24 attosecond (as), và thang thời gian của một xung quang đơn chu kỳ, khoảng một femtosecond (femto giây – một phần triệu tỷ, hay 10-15 – fs), sẽ gợi ý rằng không bao giờ có thể thăm dò động lực học electron theo thời gian thực. Trong thực tế, trong một thời gian khá dài, xung ngắn nhất được tạo ra bởi các laser phòng thí nghiệm là khoảng 6 fs. Sự phát triển thực nghiệm của các xung quang ngắn đã có mối quan hệ chặt chẽ với sự phát triển kỹ thuật trong công nghệ laser, chẳng hạn như khóa chế độ và đo lường thời lượng xung ánh sáng. Điều này đã giúp có thể thăm dò cách các nguyên tử chuyển động trong một phân tử và đặc biệt là khả năng nghiên cứu các trạng thái chuyển tiếp khó nắm bắt trong các phản ứng hóa học [2], các nghiên cứu mà Ahmed Zewail đã được trao giải Nobel Hóa học năm 1999.
Con đường dài đến với xung sáng attosecond
Trong thập niên 1980, một số nhóm nghiên cứu đã sản xuất và nghiên cứu các ion nguyên tử tích điện cao hoặc các nguyên tử không có hoặc chỉ có một vài electron. Các nhà nghiên cứu đã dựa vào các phương pháp tiếp cận khác nhau, chẳng hạn như sử dụng các nguồn ion tiên tiến và laser công suất cao. Họ đã chứng minh cách các quá trình ion hóa đa photon có thể tạo ra các ion tích điện nhiều [3].
Một câu hỏi tự nhiên được đặt ra là “các photon được tạo ra ở bước sóng nào trong các quá trình ion hóa đa photon này?” Các ion tích điện nhiều khá dễ phát hiện, còn các photon được phân giải theo phổ khó hơn.
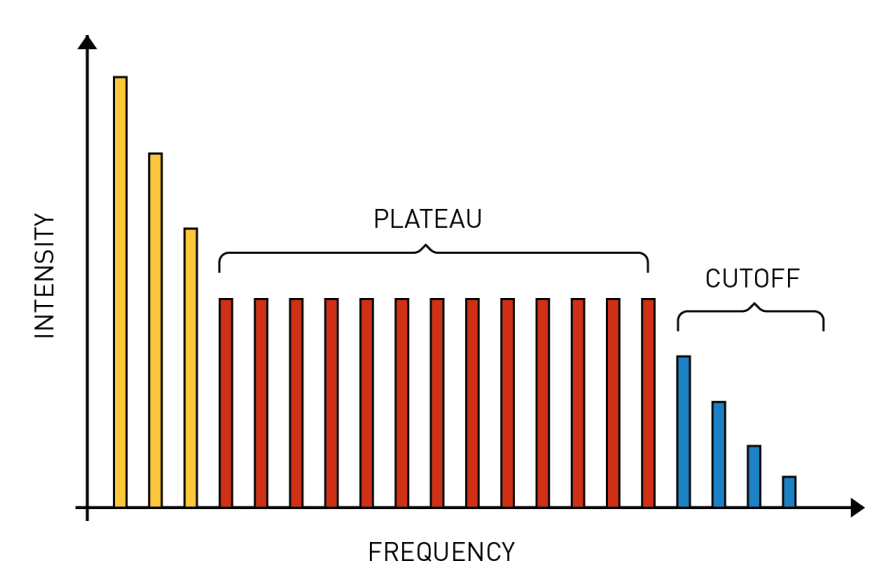
Thí nghiệm đầu tiên sử dụng photon hồng ngoại [1064 nanomet (nm) từ laser mạnh] được thực hiện tại một trung tâm nghiên cứu ở Paris-Saclay, Pháp [4] và đã mang lại kết quả rất đáng ngạc nhiên. Nhiều sóng hài bậc cao được tạo ra khi các khí hiếm tiếp xúc với photon hồng ngoại có cường độ 1013 W/cm2, tương ứng với phát xạ bức xạ liên tục ở các tần số gấp nhiều lần tần số laser. Điều đáng ngạc nhiên là cường độ phát xạ của các sóng hài lẻ ban đầu giảm khá mạnh, sau đó về cơ bản là không đổi từ sóng hài thứ 5 đến sóng hài thứ 33 đối với argon, và sau đó giảm lại. Đây không phải là lần đầu tiên quan sát thấy sự tạo sóng hài bậc cao (HHG), nhưng đây là lần đầu tiên quan sát thấy một vỉa cao rất rõ ràng. Câu hỏi vẫn còn là quá trình vật lý nào chịu trách nhiệm cho sự hình thành của vỉa cao và làm thế nào để khai thác nó. Hình 1 cho thấy cường độ phát xạ tổng quát như một hàm của tần số trong HHG.

Hình 1. Phổ tạo sóng hài bậc cao (HHG) tổng quát với ba đặc điểm đặc trưng: sự giảm cường độ ban đầu, vỉa cao và điểm cắt.
Một số nhóm nghiên cứu đã gợi ý rằng vỉa cao cung cấp độ rộng băng thông cần thiết để tạo ra các xung ánh sáng rất ngắn [5–7], nhưng các đề xuất của họ được đưa ra dưới dạng “trên nguyên tắc thì có thể”. Để sử dụng hiệu quả vỉa cao HHG, cần phải hiểu cơ chế của HHG.
Trong một bài báo được công bố năm 1991, Anne L’Huillier, Kenneth Schafer và Kenneth Kulander [8] đã trình bày kết quả từ một giải pháp số của phương trình Schrödinger phụ thuộc thời gian (TDSE), và họ đã cung cấp một sự hiểu rõ ràng về quá trình HHG. Họ đã dự đoán chính xác hình dạng chung của phổ HHG (Hình 1), nhận ra rằng HHG là một hiệu ứng electron đơn (SAE, xấp xỉ electron hoạt động đơn lẻ) và đưa ra thảo luận đầu tiên về việc ghép pha vĩ mô, đòi hỏi phải giải phương trình Maxwell.
Sau đó, nhóm của Kulander đã sử dụng TDSE SAE để suy ra một công thức đơn giản cho năng lượng cắt đối với các nguyên tử khí trơ [9]:
Ec = Ip + 3Up
Trong đó Ip là thế năng ion hóa của nguyên tử và Up là thế năng pondermotive (thế năng do dao động) của trường laser (tỉ lệ với tích của cường độ laser và bước sóng), hay nói cách khác, là năng lượng động trung bình thu được bởi một electron dao động trong trường laser.
Đầu năm 1993, tại một hội nghị ở Bỉ, Kulander đã có bài trình bày bằng miệng về mô hình rescattering (tái va chạm – một quá trình trong đó một hạt va chạm với một vật thể, sau đó va chạm lại với vật thể đó một lần nữa. Trong vật lý laser, rescattering là một quá trình quan trọng trong tạo sóng hài bậc cao (HHG)) mới được xây dựng của nhóm nghiên cứu, mô tả cách các xung ngắn trong tia cực tím cực cao (XUV), trong khoảng từ khoảng 10 đến 120 eV, được tạo ra bởi HHG [10]. Hình 2 cho thấy cách hình dung quá trình này thông qua mô hình rescattering.

Hình 2. Mô hình ba bước bán cổ điển hoặc mô hình tái va chạm của quá trình HHG. Trong bước đầu tiên, trường laser gây ra ion hóa qua hiện tượng xâm nhập xuyên hầm; trong bước thứ hai, trường laser tăng tốc electron. Khi trường đảo ngược trong nửa chu kỳ tiếp theo, electron tự do có thể trở lại ion và tái kết hợp. Trong bước thứ ba, quá trình tái kết hợp chuyển đổi năng lượng động của electron thành photon tia X rất cực vi cực (XUV) được phát xạ.
Phát hiện thú vị của Kulander và các cộng sự bắt nguồn từ công trình lý thuyết của họ về quá trình ion hóa trên ngưỡng (ATI), trong đó trường laser mạnh thúc đẩy các chuyển đổi electron tự do-tự do. Nói cách khác, electron được thúc đẩy trong liên tục trên giới hạn ion hóa đầu tiên theo các bước tương ứng với bước sóng laser. Quá trình ATI lần đầu tiên được phát hiện thực nghiệm bởi Pierre Agostini và các cộng sự vào năm 1979 [11], và ATI là trung tâm của sự chú ý trong vật lý nguyên tử laser trường mạnh trong một thập kỷ.
Vào khoảng thời gian mà Kulander và nhóm của ông đang làm việc trên mô hình tái va chạm [10], Paul Corkum [12], người cũng có nền tảng vật lý nguyên tử trường mạnh, đã xây dựng một mô hình thay thế cho mô hình đó, được gọi là mô hình ba bước. Trong cả mô hình Kulander và Corkum, thành phần quan trọng là tác động giữa electron và ion trong quá trình tái va chạm. Trong ATI, chỉ sự tương tác giữa trường laser và electron là quan trọng. Trong mô hình tái va chạm, như được minh họa trong Hình 2, electron không bị kích thích đến mức thoát ra khỏi nguyên tử. Thay vào đó, nó quay trở lại, được trường laser đẩy ngược về ion tích điện đơn mà nó bỏ lại phía sau. Trong quá trình tái hợp, năng lượng động của electron được chuyển đổi thành photon XUV khi electron quay trở lại ion.
Hình 2 cũng minh họa lý do tại sao việc khám phá vỉa cao của phổ HHG (Hình 1) được tạo điều kiện thuận lợi bởi việc sử dụng laser Nd:YAG mạnh mẽ ở 1064 nm thay vì bức xạ 248 nm được sử dụng bởi nhóm của C.K. Rhodes [13]. Bức xạ laser 248 nm buộc electron phải quay trở lại ion nhanh hơn nhiều so với ở 1064 nm, với năng lượng động ít hơn nhiều; khả năng electron phát triển vỉa cao HHG bị hạn chế hơn trong trường hợp này.
Các mô hình của Kulander và Corkum là bán cổ điển, và vào năm 1994, Lewenstein, L’Huillier và Corkum cùng một số đồng tác giả khác đã trình bày một lý thuyết lượng tử đầy đủ [14] xác nhận các giải thích bán cổ điển của Kulander và Corkum. Được trang bị sự hiểu biết vững chắc về quá trình tái va chạm, từ cả quan điểm bán cổ điển và lượng tử, L’Huillier và các cộng sự hiện có thể tiến hành di chuyển việc quan sát và hiểu biết về HHG theo hướng sử dụng nó để tạo ra các xung attosecond, được trình bày trong một loạt các bài báo seminal vào giữa đến cuối những năm 1990 [15–17].
Tạo ra xung sáng attosecond
Con đường đến với các xung attosecond đã được vạch ra và các bước lý thuyết đã được xác minh bằng thực nghiệm. Yêu cầu tiếp theo là phát triển một phương pháp đo đạc thời lượng của các xung attosecond và sử dụng các hệ thống laser phù hợp.
Một bước quan trọng đã được thực hiện bởi Agostini và cộng sự vào năm 1994 [18], nơi họ nghiên cứu nguyên tắc điều chế tần số trong trường photon hai màu. Nguyên tắc này sau đó đã được phát triển thành kỹ thuật đo lường có tên RABBIT (phục dựng xung attosecond bằng cách giao thoa của các quá trình chuyển đổi hai photon). Kỹ thuật RABBIT giúp đo thời lượng xung của một chuỗi các xung attosecond bằng cách hội tụ xung XUV và ánh sáng từ laser điều khiển vào mục tiêu khí hiếm và phân tích các electron quang điện phát ra từ mục tiêu.
Corkum, Burnett và Ivanov [19] và sau đó là Schafer và Kulander [20] cũng cung cấp những hiểu biết quan trọng. Trong bài báo đầu tiên [19], lý thuyết đã được sử dụng để đề xuất cách một trường điều khiển có phân cực phụ thuộc thời gian có thể dẫn đến việc giới hạn phát xạ sóng hài thành một chu kỳ duy nhất. Schafer và Kulander [20] cũng dựa trên lý thuyết để đề xuất rằng có thể tạo ra một xung attosecond cô lập bằng cách sử dụng xung vài chu kỳ. Phương pháp này chính xác là những gì Ferenc Krausz đã sử dụng khi tạo ra các xung attosecond cô lập lần đầu tiên.
Con đường đến các xung attosecond cô lập đòi hỏi những phát triển kỹ thuật mà Krausz đã khám phá cùng với nhóm nghiên cứu của mình ở Vienna hợp tác với nhóm của Mauro Nisoli ở Milan [21, 22]. Sự hợp tác Milan-Vienna đã dẫn đến việc tạo ra các xung ngắn nhất vào thời điểm đó: 4,5 fs, sử dụng krypton lấp đầy sợi rỗng và 5 fs với argon làm khí lấp đầy sợi. Nhóm ở Milan đã tiên phong trong kỹ thuật nén xung laser sử dụng sợi lõi rỗng chứa đầy khí. Ở Vienna, nhóm Krausz đã tạo ra một phổ HHG mở rộng với điểm cắt khoảng 300 eV [22].
Bây giờ mọi thứ đã sẵn sàng để tạo ra các xung attosecond. Năm 2001, 13 năm sau khi quan sát thấy các phổ HHG đầu tiên được điều khiển bởi laser IR [4], các xung attosecond đã được chứng minh ở Paris-Saclay và Vienna. Tại Paris-Saclay, tại cùng trung tâm nghiên cứu nơi HHG được phát hiện [4], nhóm Agostini đã tạo ra một chuỗi các xung có độ dài 250 as [23], được đo bằng công nghệ đo lường RABBIT sử dụng argon làm khí mục tiêu. Tại Vienna, nhóm Krausz đã tạo ra các xung cô lập có độ dài 650 as [24]: để làm điều này, họ sử dụng lọc phổ để chọn các sóng hài có liên quan với gương XUV nhiều lớp. Sau đó, họ đo phổ năng lượng động của các electron quang điện 4p được phóng ra từ các nguyên tử krypton dưới sự chiếu xạ đồng thời của các photon 90 eV và các xung ánh sáng ở bước sóng 750 nm từ laser điều khiển tạo ra bức xạ sóng hài (streaking).
Họ đã mở ra cánh cửa cho việc nghiên cứu động lực học electron trong nguyên tử, phân tử và vật chất trong pha ngưng tụ.
Tia điện từ bị trễ
Việc mở ra một cửa sổ thời gian mới đã giúp trả lời những câu hỏi mà trước đây không thể giải quyết được. Năm 1905, Albert Einstein đã công bố giải thích đầu tiên về hiệu ứng quang điện, nhưng vào thời điểm đó, không thể phân giải được thang thời gian liên quan đến hiệu ứng này. Trong một thời gian dài, các nhà vật lý cho rằng hiệu ứng này là tức thời.
Cuối cùng, Einstein đã được trao giải Nobel Vật lý năm 1921 “cho những đóng góp của ông cho vật lý lý thuyết, và đặc biệt là cho việc khám phá ra định luật về hiệu ứng quang điện”. Ngoài lề, khi ông có bài giảng Nobel, nó không diễn ra tại Stockholm vào tháng 12 năm 1922 (Einstein đang ở Nhật Bản vào thời điểm đó), mà diễn ra vào giữa mùa hè năm 1923, tại Gothenburg – một sự kiện độc đáo trong lịch sử của giải Nobel. Bài nói chuyện của ông không liên quan đến hiệu ứng quang điện mà là thuyết tương đối, thuyết mà ông không bao giờ được trao giải Nobel.
Câu hỏi cơ bản mà các nhà khoa học đoạt giải Nobel năm nay đặt ra là “thang thời gian của hiệu ứng quang điện là bao nhiêu?”. Khi một nguyên tử hoặc bề mặt hấp thụ đủ năng lượng từ ánh sáng tới, nó có thể truyền năng lượng đó cho một electron, sau đó electron được phát ra với động năng bằng năng lượng photon trừ đi năng lượng liên kết của electron. Động lực học phức tạp của phát xạ quang điện nguyên tử dẫn đến một độ trễ thời gian nhỏ, và câu hỏi là độ trễ thời gian này nhỏ như thế nào. Trước khi cửa sổ khoa học attosecond được mở ra, người ta có thể giả định rằng quá trình này diễn ra tức thời, vì vậy trọng tâm nghiên cứu là về năng lượng. Đây là nền tảng của phổ quang điện tử.
Nhóm Krausz [25] đã tìm thấy trong một thí nghiệm tiên phong rằng khi nguyên tử neon bị ion hóa bởi các photon 100 eV, có một độ trễ thời gian giữa việc phát ra các electron từ 2s và 2p. Electron 2p thoát khỏi nguyên tử neon chậm hơn electron 2s 21 as. Điều này có thể được so sánh với thời gian quỹ đạo tự nhiên là 100 as đối với electron 2p trong neon. Độ trễ phát xạ quang điện là dấu hiệu của động lực học tập thể của đám mây electron. Nhóm Krausz đã sử dụng các xung attosecond cô lập và kỹ thuật streaking, ghi lại động năng electron theo thời gian bù trừ giữa các xung XUV và IR.
Các tính toán lý thuyết [26–28] không thể tái tạo kết quả thực nghiệm và chúng cho kết quả ngắn hơn khoảng một yếu tố hai. Mặc dù đây là những tính toán phức tạp, nhưng các nhóm lý thuyết khác nhau đã thống nhất về các độ trễ thời gian được tính toán.
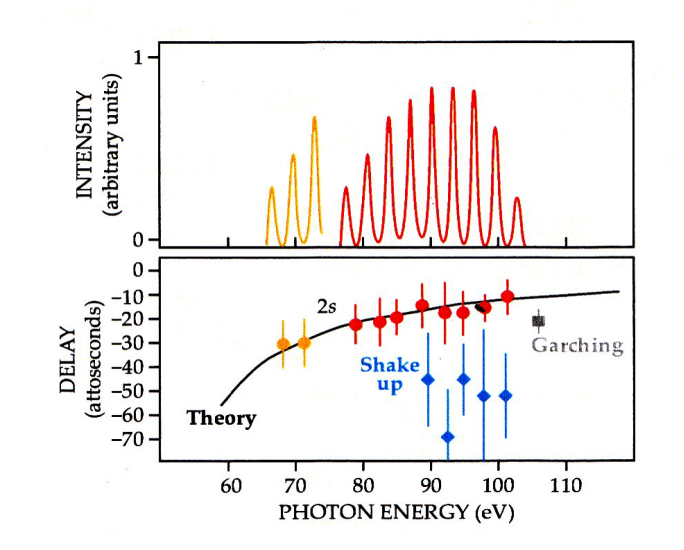
Nhóm của L’Huillier đã giải quyết sự khác biệt [29] bằng cách sử dụng phổ HHG thu được bằng cách giao thoa pha giữa các xung attosecond trong một chuỗi. Bằng cách này, các nhà nghiên cứu có thể tránh được sự đánh đổi tự nhiên giữa độ phân giải thời gian và độ phân giải phổ, như đã được chứng minh trước đây [30]. Hình 3 cho thấy thiết bị thực nghiệm mà nhóm nghiên cứu đã xây dựng ở Lund, Thụy Điển. Để tránh chồng lấn giữa các tín hiệu ion hóa từ 2s và 2p, họ đã áp dụng lọc phổ để chọn các sóng hài trải dài dưới 27 eV. Năng lượng liên kết của 2s vượt quá 2p 27 eV. Kết quả được thể hiện trong Hình 4.

Hình 3. Mô tả sơ đồ thí nghiệm ở Lund. Thí nghiệm này sử dụng kỹ thuật “phục dựng xung attosecond bằng cách giao thoa của các quá trình chuyển đổi hai photon” (RABBIT). Laser điều khiển ở bước sóng 800 nm, 30 femtosecond (fs), được gửi vào hai nhánh khác nhau bởi một bộ tách chùm tia. Phát xạ sóng hài bậc cao (HHG) trong một tia khí neon tạo ra một chuỗi các xung attosecond XUV. Các xung IR từ laser điều khiển và các xung XUV (thường có dải thông 10–20 eV) được chồng lên nhau và hội tụ bởi một gương hình xuyến vào mục tiêu khí neon. Các photon XUV ion hóa khí mục tiêu và các electron quang điện được phân tích bởi một máy quang phổ chai từ. Các xung IR/XUV chồng lên nhau tạo ra các tín hiệu dải phụ có thể phân giải các electron shake-up (với electron 2p bị ion hóa đồng thời cũng làm cho một electron 2p khác được thăng lên 3p) từ các electron 2s mặc dù có sự chênh lệch năng lượng chỉ 7,4 eV. (Hình ảnh được tải lên ResearchGate bởi David Busto, Đại học Lund.)

Hình 4. Độ trễ thời gian trong quá trình ion hóa quang điện [29] của electron 2p so với electron 2s trong nguyên tử neon ![]() . Ở phần trên, phổ HHG được sử dụng trong thí nghiệm được hiển thị. Lưu ý rằng neon được sử dụng cả cho HHG và làm mục tiêu trong máy quang phổ chai từ được đánh dấu MBES trong Hình 3. Độ trễ thời gian âm cho ion hóa 2p so với 2s được hiển thị dưới dạng các chấm màu vàng và đỏ. Kết quả thực nghiệm từ nhóm Krausz ở Garching được hiển thị dưới dạng hình vuông [25]. Các kim cương màu xanh là các độ trễ thời gian được đo giữa shake-up và ion hóa 2p
. Ở phần trên, phổ HHG được sử dụng trong thí nghiệm được hiển thị. Lưu ý rằng neon được sử dụng cả cho HHG và làm mục tiêu trong máy quang phổ chai từ được đánh dấu MBES trong Hình 3. Độ trễ thời gian âm cho ion hóa 2p so với 2s được hiển thị dưới dạng các chấm màu vàng và đỏ. Kết quả thực nghiệm từ nhóm Krausz ở Garching được hiển thị dưới dạng hình vuông [25]. Các kim cương màu xanh là các độ trễ thời gian được đo giữa shake-up và ion hóa 2p ![]() . Đường kẻ đen liền là lý thuyết với lý thuyết nhiễu loạn nhiều thân [29]. (Hình được sao chép từ Tài liệu tham khảo [31].)
. Đường kẻ đen liền là lý thuyết với lý thuyết nhiễu loạn nhiều thân [29]. (Hình được sao chép từ Tài liệu tham khảo [31].)
Sự kết hợp rất tốt giữa thí nghiệm Lund và các tính toán lý thuyết bằng phương pháp nhiễu loạn đa thể cho thấy rằng kết quả tiên phong của nhóm Krausz [25] đã bị ảnh hưởng bởi sự rung chuyển. Chênh lệch năng lượng giữa một photon đơn loại bỏ một electron khỏi 2p trong khi đồng thời thăng giáng một electron 2p khác lên lớp vỏ 3p chỉ cao hơn 7,4 eV so với năng lượng ion hóa trực tiếp của một electron 2s. Trong thí nghiệm Lund, các tín hiệu dải bên từ rung chuyển và 2s có thể được tách ra [29]. Điều này sẽ không được giải quyết trong thí nghiệm Garching. [25]
Ứng dụng trong khoa học vật liệu
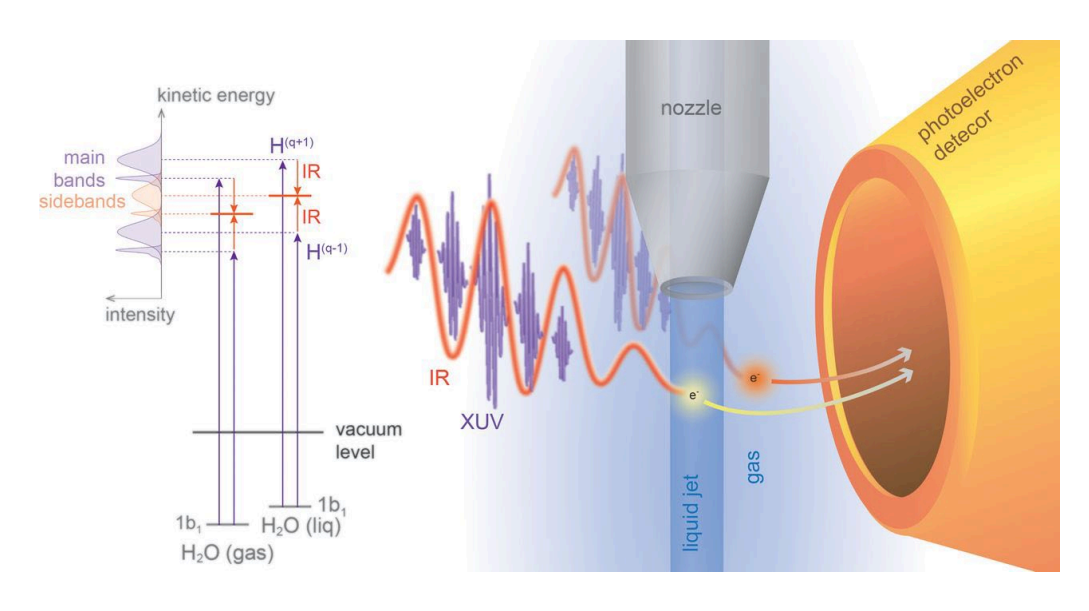
Các nghiên cứu về tương tác ánh sáng-vật chất trong miền thời gian attosecond gần đây đã mở rộng sang các lĩnh vực mới, bao gồm phân tử, chất lỏng và chất rắn. Như một ví dụ, chúng tôi sẽ mô tả ngắn gọn một thí nghiệm minh họa theo cách định lượng cách động lực học của electron phụ thuộc vào môi trường hóa học [32]. Hình 5 cho thấy thiết lập của một thí nghiệm giao thoa attosecond được thiết kế để đo độ trễ thời gian giữa phát xạ quang điện từ nước dạng lỏng và nước dạng khí.
Ở thang thời gian attosecond, tất cả các loại động lực cấu trúc đều bị đóng băng, ngoại trừ động lực của electron, và do đó thí nghiệm cho phép nghiên cứu động lực học của electron. Như Hình 5 cho thấy, một chuỗi xung attosecond chồng lên với một xung laser femtosecond gần IR được cho phép tương tác với nước trong cả pha lỏng và pha khí. Các quang điện tử được phát ra đồng thời từ các phân tử nước trong pha lỏng và pha khí, và thí nghiệm cho thấy độ trễ thời gian từ 50 đến 70 attosecond (as) giữa các quang điện tử từ nước lỏng và từ nước khí. Thí nghiệm này do đó cho phép đo định lượng thực tế rằng các quang điện tử từ nước thể lỏng đến máy dò quang điện tử muộn hơn các quang điện tử từ nước thể khí.
Chuyển động chậm hơn của các quang điện tử từ nước lỏng có vẻ hợp lý theo trực quan, vì các electron này phải di chuyển qua một cảnh quan tiềm năng phức tạp hơn, so với các phân tử nước trong pha khí. Thí nghiệm trong Hình 5 đã cho thấy hiện tượng này một cách chi tiết: các phép đo có thể cô lập hiệu ứng của solvat hóa – các phân tử nước tương tác với các phân tử nước lân cận – là nguyên nhân chính gây ra độ trễ thời gian trong động lực quang ion hóa attosecond.
Hình 5. Một chuỗi xung attosecond (màu xanh lam) bao gồm một vài bậc hài bậc cao chồng lên với một xung laser femtosecond gần IR (màu đỏ), tương tác với một tia nước nhỏ. Các quang điện tử được phát ra đồng thời từ chất lỏng và pha khí xung quanh và được phát hiện trong máy dò quang điện tử. (Hình được tái bản từ tài liệu tham khảo [32].)
Đối với chất rắn, quang phổ attosecond được kỳ vọng sẽ tiết lộ vô số các tương tác electron phức tạp, chẳng hạn như các quá trình bao gồm chuyển tải điện tích và hiệu ứng che chắn điện tích, tạo ra điện tích ảnh và tán xạ electron-electron, cũng như chuyển động điện tử tập thể. Một trong những thí nghiệm như vậy với wolfram [33] đã giải quyết được tính phức tạp của các tương tác electron trong chất rắn. Trong một nghiên cứu phát xạ quang điện trực tiếp ở miền thời gian, với độ phân giải attosecond, các nhà nghiên cứu đã có thể chứng minh độ trễ khoảng 100 as giữa phát xạ quang điện có nguồn gốc từ các trạng thái 4f giống như nguyên tử cục bộ so với những trạng thái có nguồn gốc từ các trạng thái dải dẫn lưu động. Họ đã sử dụng cái gọi là thí nghiệm bơm-dò, trong đó một xung ánh sáng ban đầu kích hoạt động lực của kim loại wolfram, tiếp theo là một xung ánh sáng thứ hai dò trạng thái tạm thời thông qua quá trình phát xạ quang điện.
Thí nghiệm này [33] đã sử dụng thực tế là năng lượng liên kết của các trạng thái 4f giống như nguyên tử khác biệt đáng kể so với các trạng thái dải hóa trị lưu động; sự khác biệt này cho phép các nhà nghiên cứu theo dõi các thang thời gian khác nhau của các loại trạng thái electron độc đáo này. Họ phát hiện ra rằng trung bình, các quang điện tử có nguồn gốc từ các trạng thái 4f cục bộ thoát ra khỏi bề mặt wolfram muộn hơn khoảng 100 as so với các quang điện tử có nguồn gốc từ dải dẫn phi cục bộ.
Hiệu ứng trễ được quan sát trong kim loại wolfram và các vật liệu tương tự xảy ra trong quá trình vận chuyển các quang điện tử bị kích thích lên bề mặt, điều này minh họa cho khả năng quan sát trực tiếp các đặc điểm của sự lan truyền gói sóng electron với độ chính xác attosecond.
Khả năng làm rung chuyển các electron trong các thí nghiệm bơm-dò và nghiên cứu phản ứng trên thang thời gian attosecond mang lại cơ hội to lớn để khám phá các hiện tượng vật lý hoàn toàn mới. Trong khoa học vật liệu, cho đến nay, chỉ những nghiên cứu ban đầu mang tính tiên phong của vật lý attosecond mới đi vào bế tắc, nhưng nhờ nghiên cứu đột phá của L’Huillier, Krausz và Agostini, người ta có thể dự đoán nhiều kết quả đáng ngạc nhiên và không trực quan sẽ xuất hiện trong tương lai. Để tưởng tượng những điều bất ngờ mà động lực học attosecond của electron có thể nắm giữ, chúng ta hãy dựa vào một số phản ứng động lực học bất ngờ mà chúng ta biết rằng các vật thể hàng ngày có, chẳng hạn như con lắc Kapitza, với khả năng tưởng như kỳ diệu của nó để chống lại lực hấp dẫn (xem ví dụ tại https://www.youtube.com/watch?v=GgYABmG_bto).
Kết luận
Nền tảng khoa học này không thể phản ánh hết chiều rộng của khoa học attosecond. Điều bắt đầu như một lĩnh vực tương đối hẹp tập trung vào các quá trình đa photon trong vật lý nguyên tử hiện đã mở rộng sang nhiều lĩnh vực tiên phong trong vật lý phân tử, hóa học vật lý, vật lý vật chất ngưng tụ và các lĩnh vực ứng dụng như công nghệ tạo ra ánh sáng. Và những bước đầu tiên hướng tới các ứng dụng sinh học đã được thực hiện bởi nhóm Krausz ở Garching.
Bằng cách kết hợp quang học băng thông rộng, các nguồn laser ultrafast và công nghệ giải quyết trường chính xác femtosecond-attosecond, nhóm Krausz đã phát triển dấu vân tay phân tử trường điện có thể phát hiện những thay đổi trong thành phần phân tử của chất lỏng sinh học. Điều này hứa hẹn như một kỹ thuật phân tích chẩn đoán in vitro mới để phát hiện các dấu hiệu phân tử đặc trưng của các bệnh trong mẫu máu [34]. Ưu điểm lớn là nhiều phân tử có thể được theo dõi cùng một lúc và bức xạ không ion hóa nên không gây hại.
Để mở rộng thêm nền tảng của khoa học attosecond, công việc quan trọng cũng đã được thực hiện bởi các nhóm khác. Xem những người của Margaret Murnane và Henry Kapteyn tại Đại học Colorado, Boulder (ví dụ [35]), và của Ursula Keller tại ETH Zurich [36].
Một bài báo tổng quan gần đây và toàn diện của Rocio Borrego-Varillas, Matteo Lucchini và Mauro Nisoli mô tả nghiên cứu của những người đoạt giải và những gì nó đã xúc tác [37]: khi khai thác các hiệu ứng laser mạnh mẽ để chuyển thời gian sang thang attosecond, họ có thể thấy electron di chuyển trong các nguyên tử, phân tử và vật chất ở pha ngưng tụ. Giải Nobel Vật lý năm nay mở ra những cánh cửa mà Heisenberg không thể tưởng tượng được, để khám phá những hiện tượng trước đây không thể quan sát được.
Tài liệu tham khảo
- Heisenberg, Z. Physik 33, 879(1925).
- https://www.nobelprize.org/prizes/chemistry/1999/summary.
- L’Huillier, L.A. Lompre, G. Mainfray and C. Manus, Phys. Rev. Lett. 48, 1814 (1982).
- Ferray, A. L’Huillier, X.F. Li, L.A. Lompre, G. Mainfray and C. Manus, J. Phys. B: At. Mol. Opt. Phys. 21, L31 (1988).
- W. Hänsch, Opt. Commun. 80, 71 (1990).
- Farkas and Cs. Tóth, Phys. Lett. A 168, 447 (1992).
- E. Harris, J.J. Macklin and T.W. Hänsch, Opt. Commun. 100, 487 (1993).
- L’Huillier, K.J. Schafer and K.C. Kulander, J. Phys. B: At. Mol. Opt. Phys. 24, 3315 (1991).
- L Krause, K.J. Schafer and K.C Kulander, Phys. Rev. Lett. 68, 3535 (1992).
- C. Kulander, K.J. Schafer and J.L. Krause, Dynamics of Short-Pulse Excitation, Ionization and Harmonic Conversion, Proceedings of a NATO Advanced Research Workshop on SILAP (Super-Intense Laser-Atom Physics), eds. B. Piraux, A. L’Huillier and K. Rzazewski (Plenum Press, New York, 1993); K.J. Schafer, B. Yang, L.F. DiMauro and K.C. Kulander, Phys. Rev. Lett. 70, 1599 (1993).
- Agostini, F. Fabre, G. Mainfray, G. Petite and N.K. Rahman, Phys. Rev. Lett. 42, 1127 (1979).
- B. Corkum, Phys. Rev. Lett. 71, 1994 (1993).
- McPherson, G. Gibson, H. Jara, U. Johann, T.S. Luk, I.A. McIntyre, K. Boyer and C.K. Rhodes, J. Opt. Soc. Am. B 4, 595 (1987).
- Lewenstein, Ph. Balcou, M. Yu. Ivanov, A. L’Huillier and P.B. Corkum, Phys. Rev A 49, 2117 (1994).
- Antoine, A. L’Huillier and M. Lewenstein, Phys. Rev. Lett. 77, 1234 (1996).
- Salières, A. L’Huillier, P. Antoine and M. Lewenstein, arXiv quant- ph/9710060 (1997).
- Bellini, C. Lyngå, A. Tozzi, M.B. Gaarde, T.W. Hänsch, A. L’Huillier, and C.-G. Wahlström, Phys. Rev. Lett. 81, 297 (1998).
- M. Shins, P. Breger, P. Agostini, R.C. Constantinescu, H.G. Muller, G. Grillon, A. Antonetti and A. Mysyrowicz, Phys. Rev. Lett. 73, 2180 (1994).
- B. Corkum, N.H. Burnett and M.Y. Ivanov, Opt. Lett. 19, 1870 (1994).
- J. Schafer and K.C. Kulander, Phys. Rev. Lett. 78, 638 (1997).
- Nisoli, S. De Silvestri, O. Svelto, R. Szipöcs, K. Ferencz, Ch. Spielmann, S. Sartania and F. Krausz, Opt. Lett. 22, 522 (1997).
- Spielmann, N.H. Burnett, S. Sartania, R. Koppitsch, M. Schnürer, C. Kan, M. Lenzner, P. Wobrauschek and F. Krausz, Science 278, 661 (1997).
- M. Paul, E.S. Toma, P. Breger, G. Mullot, F. Augé, Ph. Balcou, H.G. Muller and P. Agostini, Science 292, 1689 (2001).
- Hentschel, R. Kienberger, Ch. Spielmann, G.A. Reider, N. Milosevic, T. Brabec, P. Corkum, U. Heinzmann, M. Drescher and F. Krausz, 414, 509 (2001).
- Schultze, M. Fiess, N. Karpowics, J. Gagnon, M. Korbman, M. Hofstetter, S. Neppl, A.L. Cavalieri, Y. Komninos, Th. Mercouris, C.A Nicolaides, R. Pazourek, S. Nagele, J. Feist, J. Burgdörfer, A.M. Azzeer, R. Ernstorfer, R. Kienberger, U. Kleineberg, E. Goulielmakis, F. Krausz and V.S. Yakovlev, Science 328, 1658 (2010).
- R. Moore, M.A. Lysaght, J.S. Parker, H.W. van der Hart and K.T. Taylor, Phys. Rev. A 84, 061404(R) (2011).
- M. Dahlström, T. Carette and E. Lindroth, Phys. Rev A 86, 061402(R) (2012).
- Feist, O. Zatsarinny, S. Nagele, R. Pazourek, J. Burgdörfer, X. Guan, K. Bartschat and B.I. Schneider, Phys. Rev. A 89, 033417 (2014).
- Isinger, R.J. Squibb, D. Busto, S. Zhong, A. Harth, D. Kroon, S. Nandi, C.L. Arnold, M. Miranda, J.M. Dahlström, E. Lindroth, R Feifel, M. Gisselbrecht and A. L’Huillier, Science 358, 893 (2017).
- Marian, M.C. Stowe, J.R. Lawall, D. Felinto and J. Ye, Science 306, 2063 (2004).
- L. Miller, Physics Today 71 (1), 18 (2018).
- Jordan, M. Huppert, D. Rattenbacher, M. Peper, D. Jelovina, C. Perry, A. von Conta, A. Schild and H.J. Wörner, Science 369, 974 (2020).
- L. Cavalieri, N. Müller, Th. Uphues, V.S. Yakovlev, A. Baltuška, B. Horvath, B. Schmidt, L. Blümel, R. Holzwarth, S. Hendel, M. Drescher, U. Kleineberg, P.M. Echenique, R. Kienberger and F. Krausz, Nature 449, 1029 (2007).
- Zigman, M. Huber, K. Kepesidis, L. Voronina, F. Fleischmann, E. Fill, J. Hermann, I. Koch, T. Kolben, G.B. Schulz, F. Jokish, N. Reinmuth, W. Gesierich, J. Behr, N. Harbeck, M. Reiser, C.G. Stief and F. Krausz, Ann. Oncol. 33, S580 (2022).
- P. Christov, R. Bartels, H.C. Kapteyn and M.M. Murnane, Phys. Rev. Lett. 86, 5458 (2001).
- Eckle, A.N. Pfeiffer, C. Cirelli, A. Staudte, R. Dörner, H.G. Muller, M. Büttiker and U. Keller, Science 322, 1525 (2008).
- Borrego-Varillas, M. Lucchini and M. Nisoli, Rep. Progr. Phys. 85, 066401 (2022).









