Pythagoras, nhà triết học và toán học người Hy Lạp, là người đầu tiên đề xuất Trái đất hình cầu vào năm 500 trước Công nguyên, chủ yếu dựa trên góc nhìn thẩm mỹ của ông thay vì chỉ ra bất kỳ bằng chứng nào. Giống nhiều người Hy Lạp khác, ông tin rằng hình cầu là hình dạng hoàn hảo nhất.

Năm 350 trước Công nguyên, Aristotle (384 – 322 TCN) lần đầu tiên đưa ra một số lập luận chứng minh Trái đất hình cầu trong cuốn sách “Trên thiên đàng” (On the Heavens) bao gồm: (1) Khi con thuyền đi về phía đường chân trời, phần thân tàu sẽ biến mất đầu tiên sau đó đến cột buồm, (2) Trái đất tạo ra một bóng đen tròn trên Mặt trăng trong lúc xảy ra hiện tượng nguyệt thực, (3) Các chòm sao khác nhau sẽ xuất hiện ở những vĩ độ khác nhau [Ví dụ chòm sao Big Dipper luôn có thể nhìn thấy ở vĩ độ 41 độ Bắc hoặc cao hơn. Dưới 25 độ Nam, bạn hoàn toàn không thể nhìn thấy nó].

Trong khoảng thời gian này, nhiều nhà triết học Hy Lạp bắt đầu tin rằng thế giới họ đang sống có thể giải thích bằng những quá trình tự nhiên thay vì viện dẫn đến sức mạnh của các vị thần, và họ cũng bắt đầu thực hiện các phép đo vật lý trên quy mô lớn. Người đầu tiên xác định kích thước Trái đất là Eratosthenes. Ông đã thực hiện một phép đo với độ chính xác đáng ngạc nhiên bằng cách kết hợp kiến thức hình học với các quan sát vật lý.

Eratosthenes sinh ra tại thành phố Cyrene của Hy Lạp vào năm 276 trước Công nguyên [vùng đất này hiện nay nằm ở Shahhat, Libya]. Ông được vua Ptolemy III của Ai Cập bổ nhiệm làm thủ thư của Thư viện Alexandria vào năm 240 trước Công nguyên. Các bạn bè và đồng nghiệp đặt cho ông biệt danh là Beta [chữ cái thứ hai trong bảng chữ cái của người Hy Lạp].

Eratosthenes là một trong những học giả nổi tiếng nhất vào thời của ông với nhiều khám phá ấn tượng về thiên văn học, toán học, địa lý, triết học và thơ ca. Hiện nay, nhiều người biết đến ông với tư cách là tác giả của phương pháp sàng Eratosthenes dùng để xác định các số nguyên tố.

Thành tựu nổi bật nhất của Eratosthenes là phép đo chu vi Trái đất. Ông ghi chép chi tiết phép đo này trong một bản thảo hiện nay đã thất lạc, nhưng phương pháp mà ông sử dụng được mô tả lại bởi các sử gia và nhà văn Hy Lạp khác.

Eratosthenes tỏ ra khá hứng thú với lĩnh vực địa lý và ông muốn vẽ bản đồ thế giới. Để thực hiện điều này, ông cần biết chính xác kích thước Trái đất. Rõ ràng một người không thể đi bộ vòng quanh Trái đất để ước tính chu vi của nó.

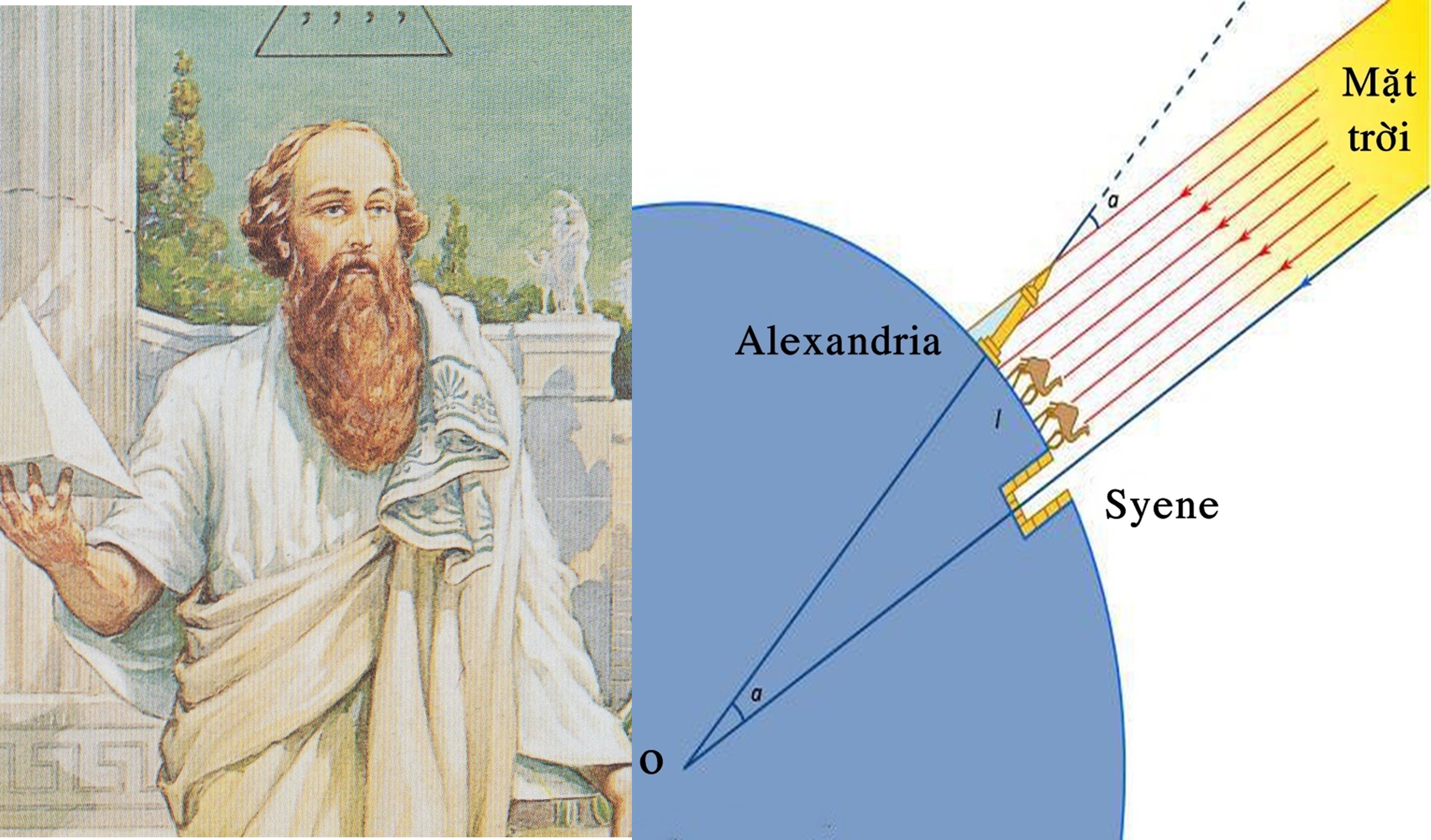
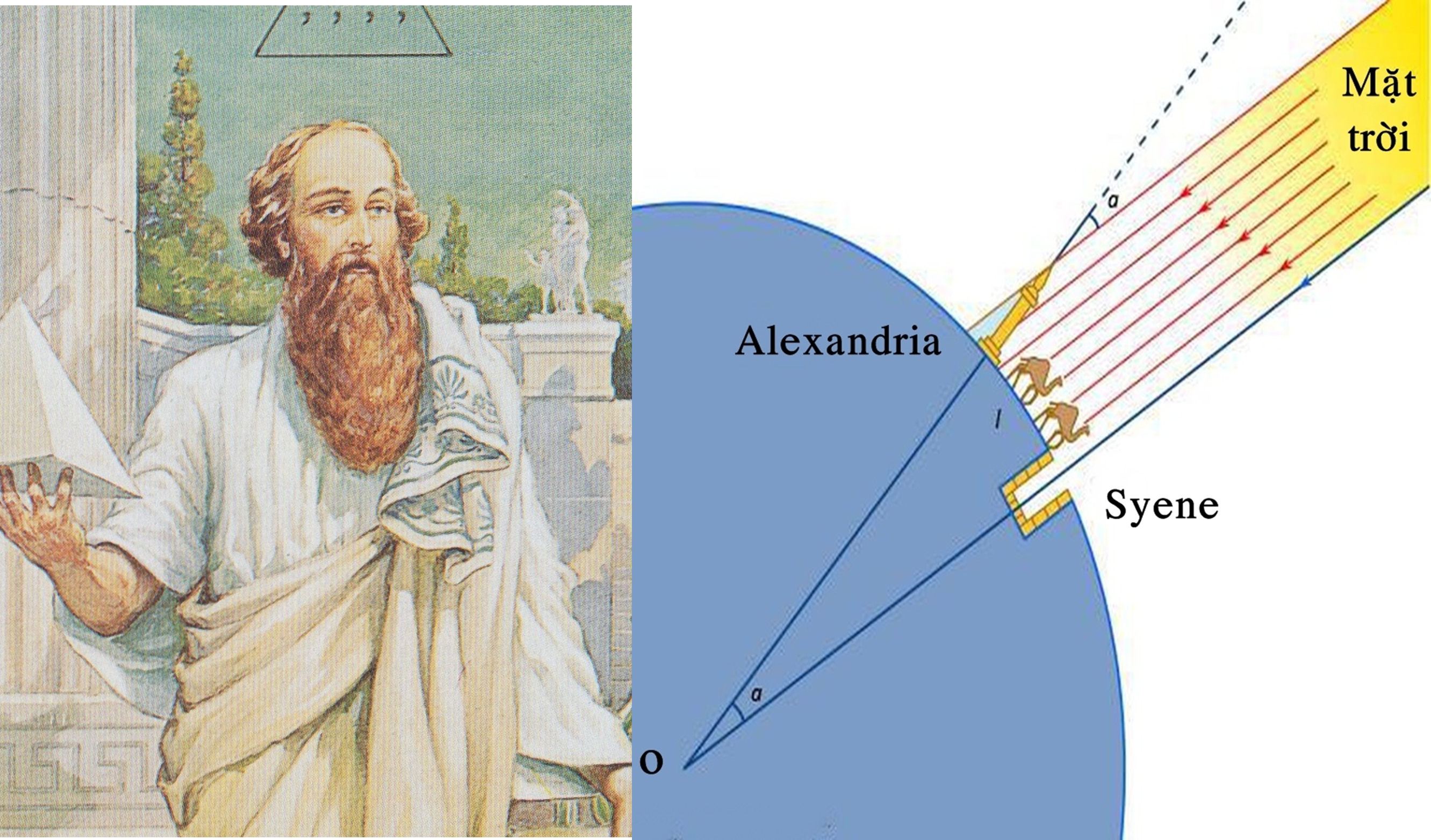
Eratosthenes từng được nghe khách du lịch kể về một cái giếng ở thành phố Syene (nay là thành phố Aswan, Ai Cập) có những đặc điểm thú vị: vào buổi trưa ngày hạ chí [ngày 21 tháng 6 hằng năm], ngay lúc Mặt trời trên đỉnh đầu, ánh sáng chiếu thẳng xuống đáy giếng mà không để lại bất kì cái bóng nào.

Để kiểm tra xem điều tương tự có xảy ra tại thành phố Alexandria [nằm ở phía Bắc thành phố Syene] hay không, Eratosthenes cắm một cây gậy thẳng đứng xuống mặt đất vào lúc giữa trưa trong ngày hạ chí. Ông phát hiện cây gậy tạo ra bóng dưới mặt đất do ánh sáng Mặt trời không chiếu vuông góc xuống Alexandria. Bằng cách đo độ dài của bóng cây gậy và độ dài thực tế của nó, ông tính được góc tạo bởi cây gậy và tia sáng Mặt trời khoảng 7,2 độ, hoặc bằng 1/50 của một đường tròn hoàn chỉnh. Theo kiến thức hình học, đây cũng chính là góc tạo bởi tâm Trái đất và vị trí của hai thành phố Alexandria và Syene.

Eratosthenes nhận ra rằng nếu biết khoảng cách từ Alexandria đến Syene, ông có thể dễ dàng tính được chu vi của Trái đất thông qua một vài phép toán đơn giản. Nhưng vào thời đó, việc xác định quãng đường giữa hai thành phố cách xa nhau với độ chính xác cao là vô cùng khó khăn. Người ta thường sử dụng thời gian một đoàn lữ hành cưỡi lạc đà đi từ thành phố này sang thành phố khác để ước tính khoảng cách của chúng. Tuy nhiên, lạc đà có xu hướng đi lang thang và đi bộ với vận tốc khác nhau. Vì vậy, Eratosthenes đã thuê các bematist [ những người được đào tạo để đi bộ với các bước dài bằng nhau. Họ tính khoảng cách bằng cách đếm số bước chân]. Kết quả cho thấy, Syene nằm cách Alexandria khoảng 5.000 stadia.

Hai thành phố Alexandria và Syene nằm cách nhau 7,2 độ trên bề mặt 360 độ của Trái đất. Khoảng cách giữa hai thành phố là 5.000 stadia [tương ứng với 7,2 độ]. Do đó chu vi Trái đất bằng (5.000 × 360) : 7,2 = 250.000 stadia.

Các học giả hiện đại không thống nhất về chiều dài của đơn vị đo “stadia” mà Eratosthenes đã sử dụng. Giá trị 1 stadia nằm trong khoảng từ 152 m đến 183 m. Do đó, chu vi của Trái đất theo cách tính của Eratosthenes nằm trong khoảng từ 38.000 km đến 45.700 km. Ngày nay, chúng ta biết rằng chu vi của Trái đất tính theo độ dài đường xích đạo bằng 40.075 km, và chu vi sẽ nhỏ hơn một chút nếu đo theo đường kinh tuyến từ cực Bắc xuống cực Nam.

Để thực hiện những tính toán nói trên, Eratosthenes giả định rằng Mặt trời ở rất xa chúng ta nên các tia sáng của nó chiếu đến Trái đất về cơ bản là song song với nhau và Syene nằm chính xác trên chí tuyến Bắc của Trái đất. Mặc dù không hoàn toàn đúng, nhưng các giả định này đủ chính xác để đo chu vi Trái đất với sai số không quá lớn. Đây là phương pháp khá đơn giản, thậm chí nó vẫn còn được các học sinh trên khắp thế giới sử dụng đến ngày nay.